Trump is actually dismantling the Department of Education! I applied for this program they have, “Presidential Scholars,” a little while ago. Seems exceptionally doubtful I’ll get it now!
One of the essay prompts said: “Please upload a photograph of something or someone of great significance to you. Explain that significance.”
Like any normal, non-psychopathic person would, I decided to write about math! Here’s the (lightly edited) essay:
Bayes’ Theorem!
This is a principle from probability that tells you how to deal with new information.
Let’s say I think a girl might like me, and want to find out exactly how likely that is. The first thing to do is find a base rate—a generic P(Like) that represents the proportion of girls that actually do like me. Maybe I’ve had the vague feeling that someone’s into me 20 times before, and only 4 of them actually were. Then P(Like) = 0.2.
Well, I’m not gonna ask this girl out based on those odds!
But the next day, she winks at me while we’re leaving a class together. That seems like good evidence that she likes me! But how good is the evidence, exactly? This, specifically this, is what Bayes’ theorem is for.
First we need to find P(Wink | Like)—the probability that a girl would wink at me given that she likes me. Well, of the 4 girls who really did like me in the past, let’s say 3 of them winked at me. So P(Wink | Like) = 0.75.
We do need to account for false positives, though. Maybe she just had something in her eye, or she was winking to the hunk behind me. We need to find P(Wink)—the generic probability of it seeming like a girl is winking at me.
Say that out of all the 20 girls I’ve thought have liked me, it looked like 5 winked at me at some time or another. (Meaning that 2 were false positives—the other 3 were the ones who winked and really did like me.) So P(Wink) = 0.25.
Now we can use Bayes’ Theorem to find the updated probability of this girl liking me after I saw her wink at me. That is, P(Like | Wink) = [P(Wink | Like) * P(Like)] / P(Wink) = [0.75 * 0.2] / 0.25 = 0.6.
Wow! The likelihood that this girl likes me has gone from 20% to 60%! I’ll probably go ask her out now.
This is all lots of fun, but I should probably give some more justification for picking Bayes’ Theorem.
One big point in favor—I actually did get a girlfriend using a process like this. That’s no small feat!
But Bayes’ Theorem is also good at solving all kinds of real-world problems. For example, breast cancer screening is extremely stressful without it. The truth is that there’s a shockingly high false positive rate—around 10%—and a true positive rate of only around 87%. This means that a positive result gives you a lot less information than you might think—and so you should worry a lot less if you get one.
Put briefly, if you come into a screening with an assumed ~0.1% chance of having breast cancer (this comes from the prevalence of new breast cancer diagnoses in American women each year—129 per 100,000), and you test positive, you should leave with an assumed ~0.9% chance of having breast cancer.
Of course, this is all subject to many more detailed features—age, other risk factors, doctor’s judgment, and so on. But Bayes’ Theorem still brings a sort of measured, calm, information-weighing attitude that keeps your stress at a proper level, your thoughts more grounded, and makes for more realistic plans of action.
Bayes’ Theorem’s awesomeness doesn’t even stop there.
There’s a school of epistemology that says, more or less, knowledge acquisition is just a matter of updating prior beliefs on new evidence. They advocate the use of Bayes’ Theorem to do that updating in a measured and correct manner, and call it, creatively, Bayesian epistemology.
Bayesians like to put numbers on their beliefs. And, to keep themselves honest, often also bet on their beliefs.
There’s a series of anecdotes in Michael Lewis’ biography of Sam Bankman-Fried, Going Infinite, that detail the culture at a quantitative trading firm SBF had interned at. The firm’s called Jane Street, and they encourage their interns to bet with one another on everything. On a game of cards or coin flip, sure, but also on who’ll call in sick how many times, or when the boss will get back from lunch, or whatever else.
This makes the interns really good at putting numbers on their beliefs. Numbers that have real meaning and are well-calibrated—things that a Jane Street intern says will happen with 80% confidence tend to happen about 80% of the time.
Jane Street trades with around $15 billion in capital each year, and makes a profit of about $7.5 billion. 50% returns are incredibly good! And they’re capable of it, in no small part, because they’ve built a culture that cares deeply about Bayesian reasoning . A culture that tells you to put numbers to your beliefs, and carefully update them according to mathematical logic.
Bayesian epistemologists have their fingers in a lot of pies.
Not only do they dominate successful quant firms—they’re also at the forefront of the emerging phenomenon of prediction markets and forecasting tournaments.
Companies like Manifold, Polymarket, and Metaculus have popped up to offer users the chance to bet play money, real money, or pride (respectively) on the outcomes of real-world events.
Each event becomes a market, and each forecaster buys either a stake in “yes” or “no.” The market aggregates all the different predictions, and the prices of the “yes” and “no” shares tell you the probability of an event happening.
And that probability tends to be extremely accurate! More accurate than pundits for political events, more accurate than analysts for sports events, and even more accurate than intelligence agencies at predicting the outcomes of geopolitical turmoil.
Works like The Wisdom of Crowds by James Surowiecki, and Superforecasting by Philip Tetlock explain this phenomenon, and fit squarely into the tradition of Bayesian epistemology.
It’s an old truism that you can’t predict the future—Bayesians disagree. Or, at least, they think you can assign well-calibrated probabilities to future events. And, so far, the experimental results bear them out.
The world is an extremely complicated place.
It feels intuitively that reducing the wide array of possibility space down to simple numbers should be impossible. Feels like the Bayesians must be missing something, like it must not be possible to take Bayes’ Theorem from pet examples—like my contrived dating life—to real-world events—like how a market will move, or who’ll be elected president.
And yet!
It just works. If you’re careful and thoughtful and appreciate complexity—you can do it. You can put real, reasonable, calibrated probabilities on events that initially seem totally inscrutable.
The power of Bayes’ Theorem is awesome, in the Biblical sense. Since I learned it, and since I started reading books like Superforecasting, I’ve been trying to use it everywhere I can.
Bayesian epistemologists have a saying: “shut up and multiply.” When you feel overwhelmed, when it feels like there can’t possibly be an answer, when you have lots of very strong opinions without much evidence… take a moment. Shut up. Put numbers to your beliefs. Put numbers to the evidence. And multiply.
Every day, I try to live my life more closely to that principle.
Lukethoughts
“Don’t step on the M at U of M! A piano fell on me 3 seconds after” (Ed. note: Many such cases.)
“I’m leaving for Dubai today; viewers wish me luck!!!” (Ed. note: This is a Classy Substack, we call you readers here.)
“Don’t worry the lukethoughts will remain it doesn’t matter.” (Ed. note: What a pro!)
“SHABBAT SHALOM” (Ed. note: Literal racism.)
Arithoughts
(I have a couple mini announcements, so here’s a temporary thing!)
Spring Break has finally begun!
I recycled today’s post because I spent all my brainpower last night arguing about politics on Discord and doing a stupid homework assignment about a stupid play. Also I’m still sick! Endless excuses over here.
Good, fresh essays will return soon! Tomorrow’s reserved for Torah Study, but here’s a sneak peek for Monday:


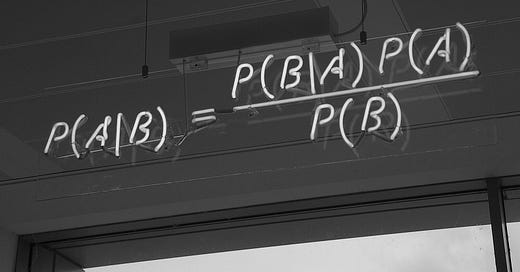




Based on this, you could almost call it bae’s theorem.
Math!
Now that I actually know what Baye's theorem is, I wonder how you applied it in your math IA. I recall you looking at SAT data and race, so is it something like "how does your chance of getting into college change based on SAT" across races?
I like math—write more math posts.